This was a project that was worked on during my time doing graduate research. At the time, our computing cluster had C++ with some fairly old compilers. We wanted to use a Mixture Density Network in a project, and the neural network libraries we were using at the time couldn’t be used that way. So, I was assigned the task of writing a Mixture Density Network in C++ from scratch.

In order to keep the code compatible with our computing cluster, I used no outside libraries. The code I created wasn’t exactly the best optimization, but since it used all basic C++ code, we didn’t have to worry about dependency issues.

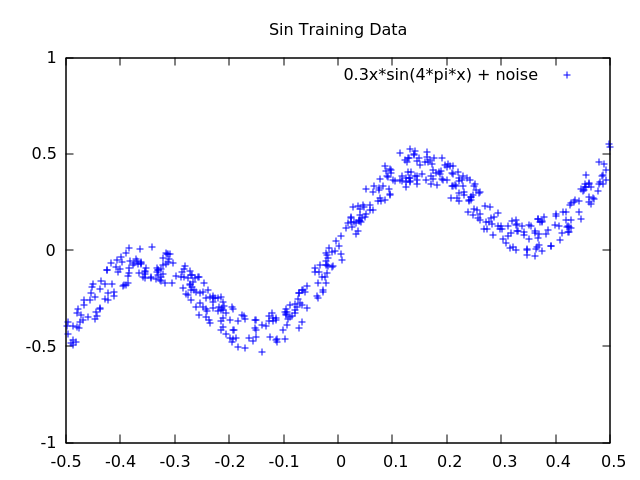
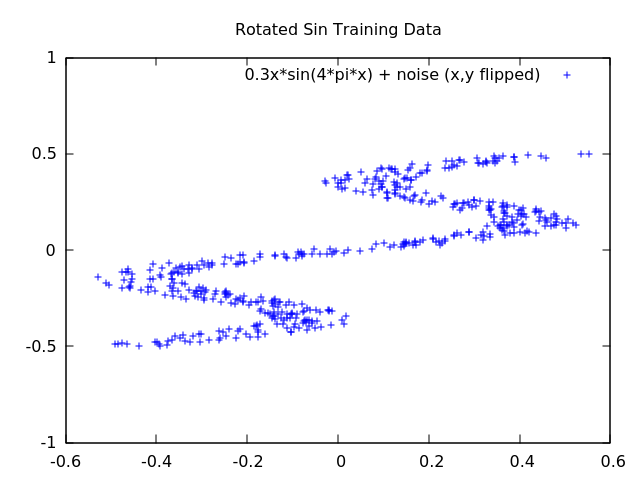
The example I used to test the Mixture Density Network was a sin function of \(0.3x \sin(4 \pi x)\). To create a data set, I made data points along the x axis of this function and added random noise to y axis values. The data points were then rotated by swapping the x and y values. As can be seen in the figures below, Figure 1 appears to be a fairly normal looking sin wave where an x value maps to a single y value. However, Figure 2 is different. In Figure 2, there are several places in the plot that multiple y values map to a single x value.

Sin Data Sin Rotated Data
Figure 1 Figure 2

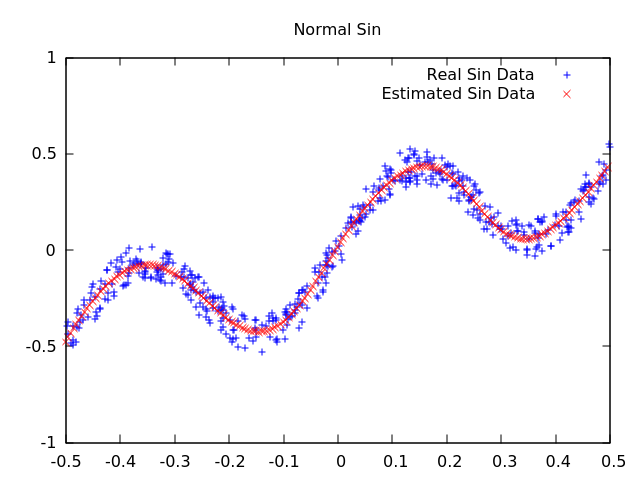
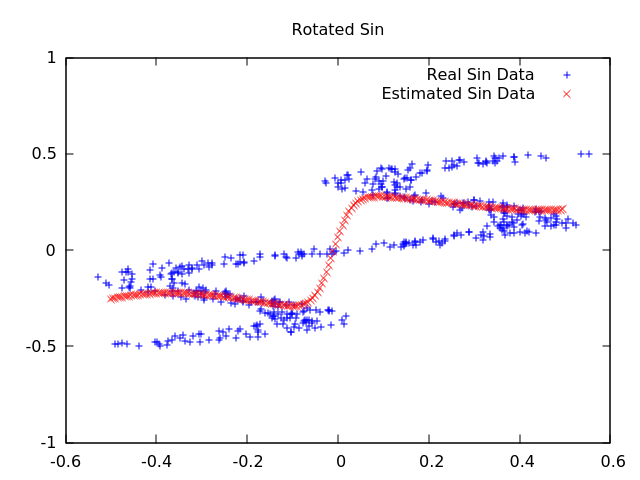
The neural network library that we were using at the time was called Fast Artificial Neural Network Library (FANN). This network didn’t support Mixture Density Networks. I created an example using FANN to demonstrate the problem. I created two neural networks and used them to try and fit the training data in Figures 1 and 2. The results are shown below.

Sin Data Sin Rotated Data
Figure 3 Figure 4

As can be seen in Figure 3, the network fits the sin function correctly. However, in Figure 4, it fails to fit the rotated function. This is due to the multi-modal nature of x mapping to multiple y points. In a trained neural network, when you input a value, you receive only a single value back, and that value shouldn’t change unless the network is trained again. So, how do we input an x value and get back multiple y values? We will use a Mixture Density Network. A paper was published on Mixture Density Networks by Christopher M. Bishop, and was later included in his book Pattern Recognition and Machine Learning.

The Mixture Density Network makes use of Gaussian Mixture Model to create the multi-modal output. A Gaussian Mixture Model is a collection of Gaussian Distributions. In a Mixture Density Network, rather than having the neural network output values, it outputs Gaussian Mixture Model parameters. These parameters are used to sample values from the Mixture Model. Each Gaussian Distribution in the Mixture Model has a probability parameter associated with it which is the probability that that particular distribution will be used. This is one of the three parameters that the neural network learns. The second and third parameters are the mean and variance for the Gaussian Distribution, which determines the actual value of the number sampled.

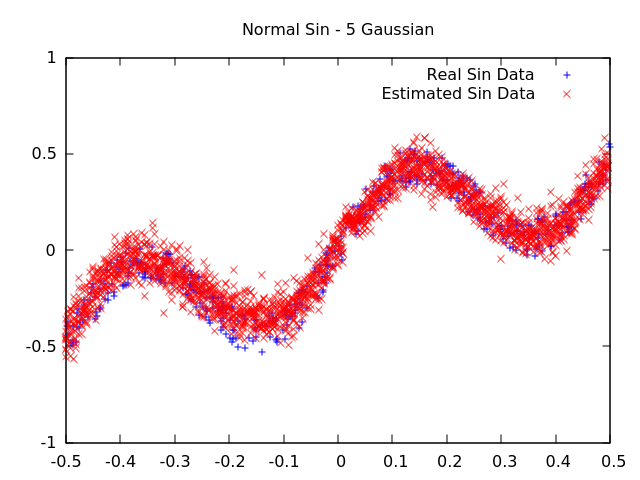
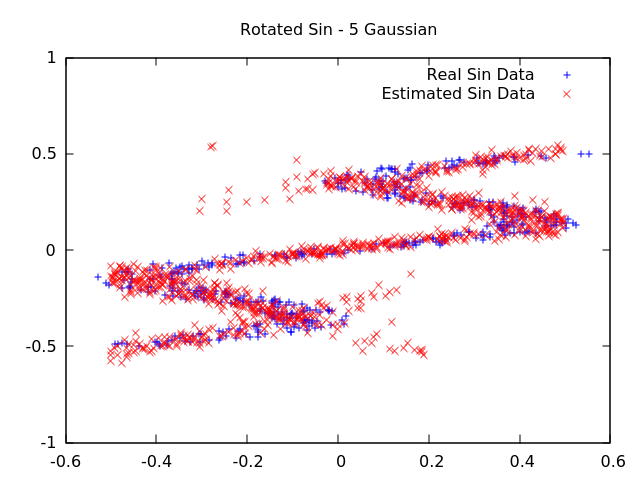
The results of the Mixture Density Network on the previous problems are shown below. In Figure 5, the normal sin data is fitted. The fit of Figure 5 is different than Figure 3. In Figure 3, each input x value output a single y value, so the data fitted resembles a line. In Figure 5, each input x value can output multiple y values, so the network fitted to imitate the noise in the network rather than the actual sin function. In Figure 6, the Mixture Density Network was able to fit the rotated sin function where the normal neural network in Figure 4 failed.

Sin Data Sin Rotated Data
Figure 5 Figure 6

The code for this project is available on my Github page.